zkFOL:承諾原生隱私與DeFi的Bitcoin軟分叉
十多年來,Bitcoin 一直維持著表面上的簡單。其 Script 語言經過刻意限制,為了安全性而犧牲了表達能力。與此同時,Ethereum、Solana 和 Avalanche 則因提供可編程的智能合約,吸引了數千億美元的流動性。但這種表達能力也帶來了漏洞:重入攻擊、不可預測的執行成本、關鍵性攻擊。

In Brief
- zkFOL 為 Bitcoin 帶來原生 DeFi 及隱私功能,且不破壞其安全模型。
- 數學上的突破將一階邏輯轉化為可驗證多項式,使複雜智能合約成為可能。
- ModulusZK 的方法提供快速證明、真正的可編程性,以及未來 Bitcoin 軟分叉的路徑。
如果 Bitcoin 能夠兼得兩者優勢會怎樣?這正是 zkFOL 所承諾的——來自 ModulusZK 的革命性軟分叉概念,為 Bitcoin 帶來原生 DeFi 和隱私,同時不損害其基本理念。這項創新既不依賴高風險的權宜之計,也不依賴聯邦側鏈。它建立在一項重大的數學突破之上:一階邏輯的算術化。
問題所在:Bitcoin Script,一種刻意受限的語言
Bitcoin Script 的設計目標是可預測且安全。沒有迴圈、沒有遞迴、沒有可變的全域狀態。每筆交易都在確定性的時間內驗證,確保網路不會因無限計算而被阻塞。正因為這種嚴謹,Bitcoin 在共識層從未遭遇重大漏洞。
但這種保守也有代價。Bitcoin Script 無法:
- 在交易之間儲存狀態
- 執行複雜的條件邏輯
- 處理多方合約,否則需極為繁瑣的手動腳本
- 支援 64 位元算術或浮點數
因此,99% 的 DeFi 創新都在其他地方誕生。開發者若想創建 AMM、借貸協議或複雜金庫,只能遷移到 Ethereum,或建立側鏈——即使 Bitcoin 擁有壓倒性的市值,其主導地位也因此被稀釋。
突破:將邏輯算術化以實現可驗證性
zkFOL 的解決方案建立在一項優雅且深刻的數學洞見之上:將邏輯直接轉換為多項式。
在現代密碼學中,算術電路(有限域上的乘法與加法組合)已取代傳統布林電路,原因很簡單:多項式可以簡潔地驗證。得益於 Schwartz-Zippel 引理,只需在隨機點驗證多項式是否為零,即可以極低的錯誤機率證明其等式成立。
Dr. Murdoch Gabbay 近期在算術化領域的研究證明,可以將任何一階邏輯謂詞(FOL)直接轉換為有限域上的等價多項式。具體來說:
- 邏輯合取(∧)變為加法
- 析取(∨)變為乘法
- 全稱量詞(∀)轉換為有限和
- 存在量詞(∃)變為有限積
結果:複雜的邏輯謂詞編譯為單一多項式,其驗證僅需在隨機點評估並檢查是否為零。這一驗證過程耗時常數時間,與謂詞初始複雜度無關。
從理論到實踐:ModulusZK 的方法
雖然數學基礎來自學術研究,ModulusZK 團隊正將這一突破轉化為生產系統。由化名 Mr O’Modulus 創立——他也是軟分叉提案的作者——ModulusZK 正在構建他們稱之為 Layer X 的證明協調層,將 FOL 算術化應用於多個區塊鏈場景。
Bitcoin zkFOL 的實現是其更宏大願景的一個應用:他們不是再造一條競爭鏈,而是創建能增強現有網路的通用證明基礎設施。
zkFOL 的實際運作方式
zkFOL 系統將 Gabbay 的算術化直接應用於 Bitcoin,採用兩階段方法:
第一階段:1:1 錨定的 Layer-2 架構
zkFOL 初期作為錨定於 Bitcoin 的 Layer-2 運作:
- 用戶將 BTC 鎖定於 Bitcoin 區塊鏈(Layer 1)上的透明多重簽名金庫
- 他們在 zkFOL 層獲得 wBTC-FOL(與鎖定 BTC 1:1 對應)
- 所有 DeFi 交易(兌換、借貸、收益農場)均在鏈下以零知識證明執行
- 證明承諾定期錨定至 Bitcoin,保證數據可用性
- 提款時,經密碼學驗證最終狀態後釋放 BTC
與現有方案不同,zkFOL 不依賴可信驗證者。驗證完全基於數學。
第二階段:軟分叉整合(未來)
一旦作為 Layer-2 被證明安全高效,長遠目標是透過軟分叉——向下兼容的協議升級——將多項式驗證直接引入 Bitcoin 基礎層。
編譯流程:邏輯 → 多項式 → 證明
每個 zkFOL 合約均以一階邏輯指定。例如,一個恆定乘積 AMM 可簡單寫為:
∀X. (Δreserve_A × Δreserve_B = k) ∧ (fees ≤ 1%)
此公式自動編譯為:
- 一個多變數多項式,每一項編碼一個約束
- 一個隱藏係數的密碼學承諾
- 一個零知識證明(zkSNARK),證明該多項式在驗證點的值為零
驗證者只需:
- 在隨機點計算評估值
- 驗證多項式承諾
- 確認結果為零
全部在常數時間內完成,無論合約多複雜。
為何這很重要:電路優先範式陷阱
整個 ZK 行業一直陷於 ModulusZK 所謂的「電路優先範式」——試圖讓算術電路更高效,而不是質疑電路是否為正確的抽象層。
傳統 ZK 方法(zkSync、StarkNet、Polygon):
// 開發者必須手動撰寫 200+ 個電路約束
circuit SwapCircuit {
// 每個操作都需手動寫約束
assert(user_balance_before.usdc >= usdc_amount_in);
assert(user_balance_after.usdc == user_balance_before.usdc – usdc_amount_in);
// … 還有 200+ 個約束
問題:
- 需要專業電路工程師(年薪超過 20 萬美元)
- 證明生成時間 5-30 秒
- 固定結算模式(zkSync → Ethereum 僅限)
- 單體設計將邏輯鎖定於證明系統
ModulusZK 的 zkFOL 方法:
自然邏輯規範——任何人都能這樣寫:
swap_valid = ∀swap_event.(
balance_conserved(swap_event) ∧
price_fair(swap_event) ∧
user_authorized(swap_event)
ModulusZK 的論點是,電路本來就不是必需的。Dr. Gabbay 的革命性發現是,邏輯有效性與多項式評估在數學上是對偶的——你可以直接在兩者間轉換。
Bitcoin 的具體應用:無妥協的 DeFi
具隱私流動性的 DEX 和 AMM
自動化做市商(類 Uniswap)可在 zkFOL 上原生運作。x × y = k 不變式成為由多項式驗證的邏輯謂詞。交易者提交訂單,驗證者生成證明以證明不變式被遵守,交易即執行——無需透露金額或對手方。
協議費用自動收取,LP 以密碼學方式驗證獲得其比例分成。
具動態比率的抵押借貸
去中心化借貸協議要求 collateral / debt ≥ minimum_ratio。在 zkFOL 中,這一比率成為多項式約束:
∀X. (collateral_amount(X) ≥ ρ × debt_amount(X))
無需持久合約或外部預言機。每筆貸款都產生一個證明,證明比率被遵守。還款則產生另一證明釋放抵押品。一切皆本地、確定且即時可驗證。
具條件邏輯的多重簽名金庫
現有 Bitcoin 金庫僅限於簡單多簽(2-of-3、3-of-5)。zkFOL 允許任意支出條件:
(owner_signature ∧ delay < 1_year) ∨
(heir_signature ∧ delay ≥ 1_year) ∨
(3-of-5_trustees ∧ emergency)
每個子句編譯為額外多項式項。驗證確認至少有一個分支被滿足。結果:可編程繼承、緊急恢復與機構託管——僅需幾行邏輯。
市場比較
| Feature | zkSync/StarkNet | Aztec Privacy | ModulusZK zkFOL |
| Developer Experience | 電路工程 | 自定語言(Noir) | 自然邏輯(FOL) |
| Proof Generation | 5-30 秒 | 10 秒以上 | 約 1-3 秒(預估) |
| Privacy Model | 無/有限 | 隔離隱私池 | 可組合 + 合規 |
| Settlement Flexibility | 固定(L2→L1) | 固定 | 動態多鏈 |
| Stablecoin Optimization | 無 | 無 | 原生支援 |
超越 Bitcoin:Layer X 願景
雖然 zkFOL 展示了這項技術在 Bitcoin 上的應用,ModulusZK 更宏大的 Layer X 願景則是:創建一個可跨所有區塊鏈運作的通用證明協調層。
傳統區塊鏈架構強制層級依賴:
- L3 需要 L2
- L2 需要 L1
- 每一層都被困於這個結構
Layer X 打破了這一模式。它不是另一個 L1、L2 或 L3——而是正交於傳統層級,提供任何鏈都能使用的證明基礎設施:
Users → Create proof → Choose where to send it:
├── Ethereum (for security)
├── Celestia (for cheap storage)
├── Solana (for speed)
└── Any other chain (for specific needs)
推動 Bitcoin zkFOL 的同一 FOL 到多項式轉換,也能推動:
- 跨鏈 DeFi
- 多鏈遊戲
- 不同網路間的機構結算
- 隱私保護型穩定幣系統(如與 Plasma 的合作提案)
推動 Bitcoin DeFi 復興的催化劑
若 zkFOL 得以推進,Bitcoin 有望重新奪回流向其他鏈的 DeFi 流動性。其優勢巨大:
- 近 2 兆美元市值變得可編程
- Bitcoin 交易量提升,透過 zkFOL 結算增加礦工手續費收入,強化長期挖礦安全
- 開發者可用形式邏輯編程,比 Solidity 更安全、可審計
- 原生隱私,無需可疑的混幣器體驗
該項目正處於開發階段,產品計劃於 2026 年推出,但路線圖明確,數學基礎堅實。與許多僅靠模糊承諾的加密項目不同,zkFOL 建立於已發表的學術成果之上。
與 Bitcoin 哲學的一致性
ModulusZK 的 zkFOL 並不尋求將 Bitcoin 變成「Ethereum 殺手」。它強化了 Bitcoin 的創始原則:
- 簡單性:複雜性外部化於證明,協議共識保持精簡
- 安全性:無新增密碼學假設,無新增攻擊面
- 自願參與:不想用 zkFOL 的用戶不受影響
- 可預測性:驗證成本確定且有上限
創新不是對抗 Bitcoin,而是與 Bitcoin 共進。這是其腳本模型的自然數學演進,而非架構上的斷裂。
化名創辦人:Mr O’Modulus
如同 Satoshi Nakamoto,ModulusZK 創辦人以「Mr O’Modulus」化名運作——他也是 BitLogic 白皮書的作者。這種做法呼應了 Bitcoin 的起源:讓數學本身勝過個人身份。
這項創新全賴於 Dr. Murdoch Jamie Gabbay——Alonzo Church Prize 得主(邏輯與計算領域的權威獎項),也是 ZK 領域被低估的先驅。這種化名願景與學術嚴謹的結合,帶來了獨特的公信力:這項技術不僅是工程改進,更是邏輯與計算互動方式的根本突破。
當數學調和安全與表達力
多年來,加密產業接受了一個偽命題:要麼選擇 Bitcoin 的嚴格安全,要麼選擇 Ethereum 的表達力及其漏洞。zkFOL 證明這種妥協並非必然。
通過將一階邏輯算術化並編譯為可零知識驗證的多項式,ModulusZK 的方法讓 Bitcoin 變成能承載完整 DeFi(兌換、借貸、金庫、收益)的網路,無需犧牲確定性或引入新攻擊向量。
這不是額外的抽象層,也不是另一條側鏈。它是 Bitcoin 的自然數學擴展,與其哲學一致,受益於應用密碼學的最新進展,並具備重大顛覆潛力。
Bitcoin 無需成為 Ethereum。有了 zkFOL,它能變得更好。成為它自己。
免責聲明:文章中的所有內容僅代表作者的觀點,與本平台無關。用戶不應以本文作為投資決策的參考。
您也可能喜歡
黑天鵝將至?美債引發連鎖危機!機構+央行已然行動,你該如何應對?
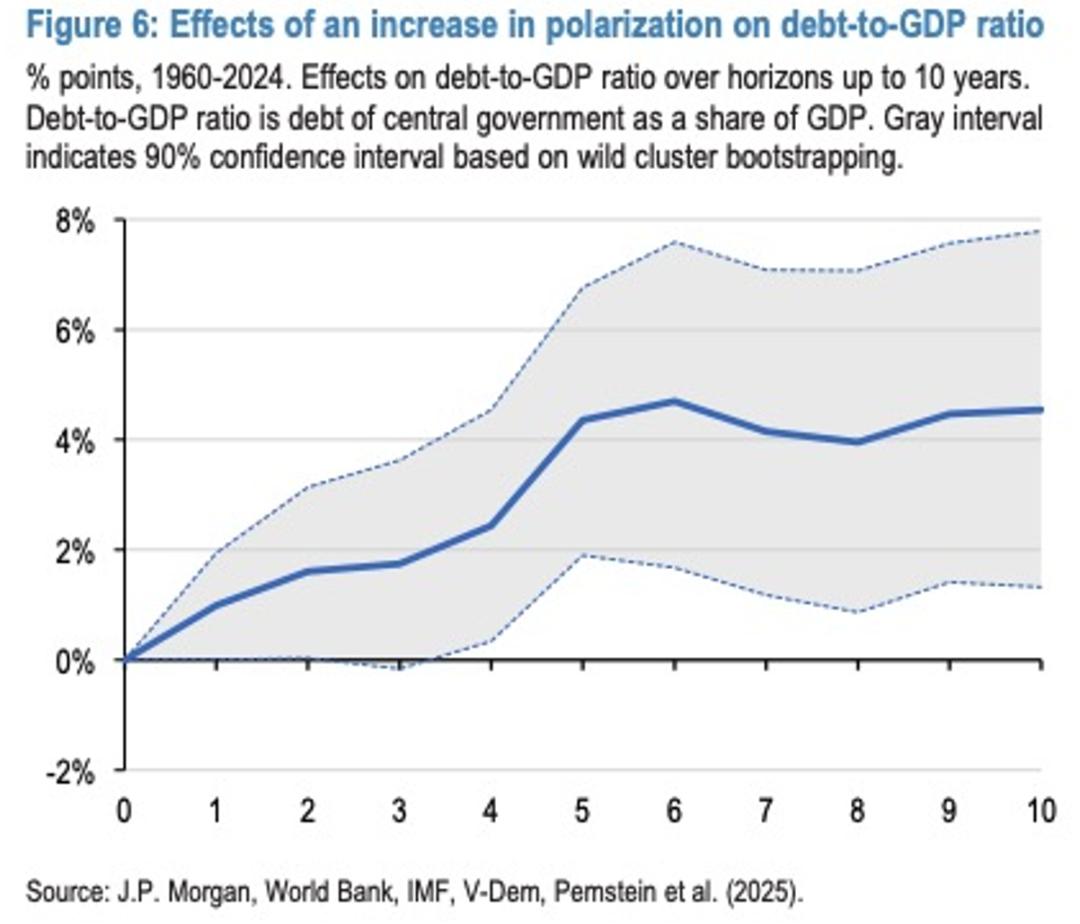
一週展望:美國PCE數據來襲,聯邦儲備庫克案受審,黃金能否延續高位神話?
Solana DEX Jupiter 推出 JupUSD,將原生國庫收益返還給用戶
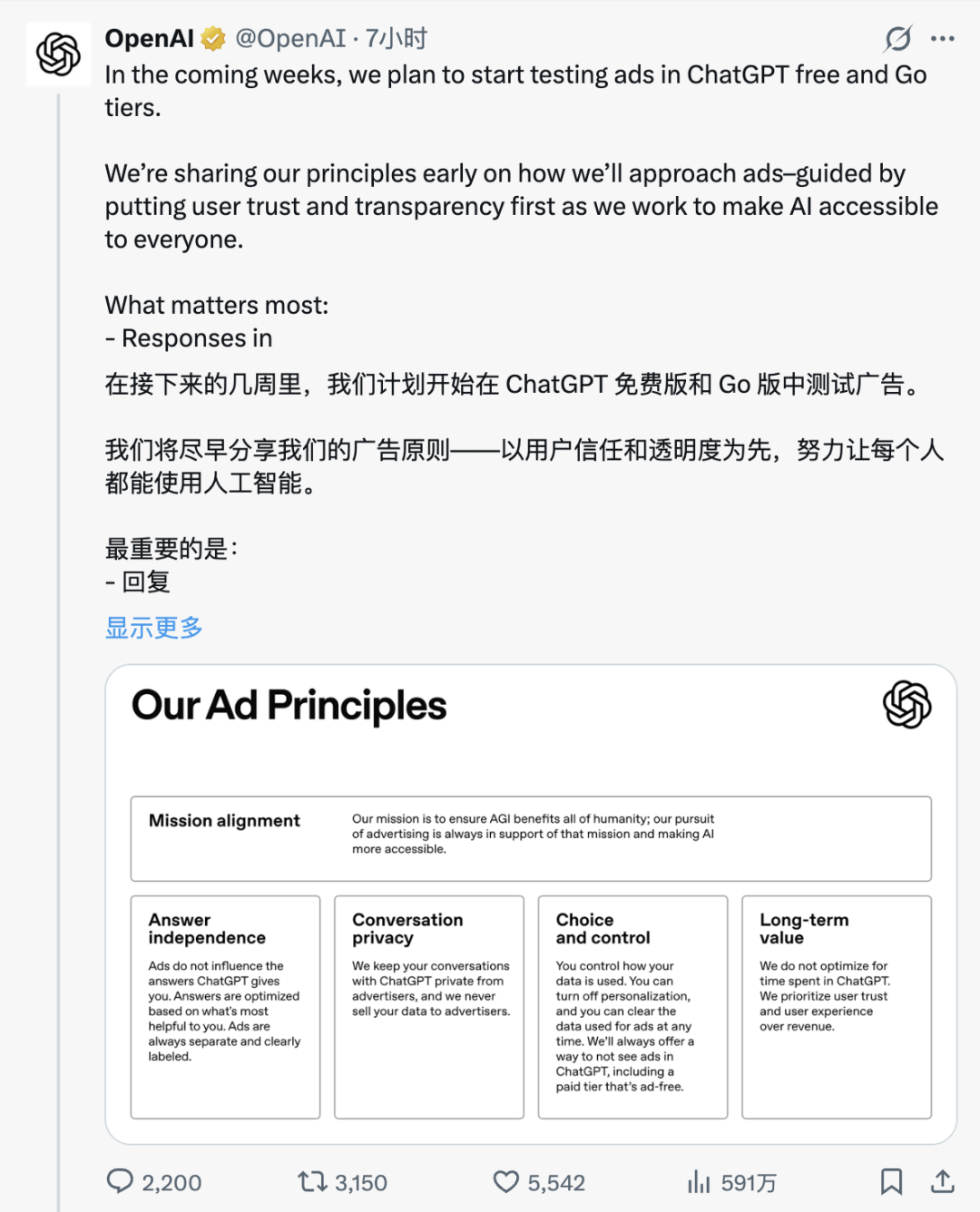
ChatGPT 突然官宣加廣告,8 美元訂閱套餐也躲不掉