L’IA va-t-elle encore bouleverser les mathématiques ? Terence Tao prend la parole d’urgence : arrêtez de diviniser !

  Rapport de Nouvelle Intelligence  

Vous êtes peut-être tombé sur ce type de titre sensationnaliste : « L’IA a résolu de façon totalement autonome un problème mathématique resté sans solution pendant cinquante ans ! Les mathématiciens vont être au chômage ! »

Pour ceux qui aspirent à assister à la naissance de l’AGI, c’est sans doute un puissant stimulant. Tandis que pour les mathématiciens soucieux de préserver la dignité de l’intellect humain, cela ressemble à l’alerte annonçant la chute du dernier bastion.

Avec l’influence croissante de ces articles, certains n’ont finalement plus pu rester silencieux et sont intervenus pour calmer le jeu.

Fait intéressant, cette personne est justement l’un des plus ardents promoteurs de la recherche mathématique par IA — Terence Tao.

Terence Tao ne nie pas la capacité de recherche mathématique de l’IA, il souhaite simplement ramener la température à la réalité.

C’est justement cette nuit que Terence Tao a publié un message, affirmant que les capacités de l’IA à résoudre des problèmes mathématiques sont exagérées de manière hors contexte.

Il a ajouté des explications et avertissements plus systématiques sur la page GitHub associée au projet Erdős Problems.

Il souligne que l’interprétation externe des solutions de l’IA aux problèmes d’Erdős est facilement excessive, surtout lorsqu’un succès isolé est pris comme preuve que « l’IA possède déjà des capacités mathématiques avancées ».

Que cherche vraiment à clarifier Terence Tao ? Jusqu’où l’IA est-elle parvenue avec les problèmes d’Erdős ?

Tout d’abord, il faut préciser que Terence Tao ne nie pas les progrès de l’IA en mathématiques.

Ce qu’il rejette surtout, c’est une certaine narration simpliste : transformer « l’IA peut produire des résultats vérifiables sur certains problèmes » en « l’IA sait déjà faire des mathématiques, peut innover toute seule et remplacer les humains ».

Sur sa page mise à jour « AI contributions to Erdős problems », il précise que lors de l’évaluation des performances de l’IA sur les problèmes d’Erdős, il ne faut pas se focaliser uniquement sur le nombre de problèmes résolus, et prêter attention notamment aux points suivants :

• La difficulté des problèmes varie énormément, le « nombre de solutions » n’est pas directement comparable : l’éventail de difficulté des problèmes d’Erdős est très large, allant de défis reconnus comme extrêmement difficiles à un grand nombre de « questions de longue traîne » peu étudiées et rarement réexaminées. Parmi ces dernières, beaucoup sont en fait des « fruits à portée de main », plus adaptées aux outils actuels d’IA. Le problème est que, sans une revue experte de la littérature, il est difficile de déterminer à l’avance la catégorie d’un problème. Ainsi, comparer « qui en résout le plus » revient souvent à comparer des niveaux de difficulté très différents.

• Pour beaucoup de problèmes, le fait qu’ils soient « non résolus » est lui-même incertain : de nombreux problèmes sur le site manquent de revue systématique de la littérature, donc l’étiquette « Open » (non résolu) est souvent temporaire. Lorsqu’une IA résout un problème, on découvre souvent rapidement que — la littérature avait déjà apporté une solution (peut-être avec une méthode légèrement différente). Cela rend la narration de « première solution par l’IA » très fragile.

• Nous voyons surtout les cas de succès, les échecs sont cachés : le site n’enregistre pas de façon exhaustive les tentatives des outils IA, et encore moins les essais sans résultat ou ratés.

• Certains énoncés de problèmes comportent des erreurs et peuvent être « contournés littéralement » : dans de rares cas, l’énoncé du problème par Erdős peut manquer de rigueur ou être erroné ; pour restituer l’intention initiale, il faut souvent s’appuyer sur le contexte et l’expérience du domaine — cette étape implique une part de subjectivité.

• La valeur mathématique ne réside pas uniquement dans la réponse, mais aussi dans la « connexion du réseau de connaissances » : le sens des mathématiques ne s’arrête pas à la preuve d’un énoncé, mais aussi à l’inspiration qu’il apporte au domaine concerné, à sa connexion avec la théorie existante et aux méthodes transférables qu’il introduit. Lorsqu’un humain rédige une preuve, il ajoute naturellement du contexte, des motivations, des comparaisons bibliographiques, des limites méthodologiques. Mais les preuves dominées par l’IA manquent souvent de cet « halo » de connaissances, et sont donc techniquement valables mais de moindre valeur pour la communauté mathématique.

• Résoudre un problème de longue traîne ne veut pas dire qu’il est digne d’une revue scientifique prestigieuse : chaque problème non résolu résolu ne vaut pas forcément une publication. Surtout si le problème est très marginal ou que la méthode n’est qu’une légère adaptation d’une technique existante, il n’atteindra probablement pas les meilleures revues.

• Formaliser une preuve générée par IA dans un assistant comme Lean augmente la fiabilité, mais il reste possible de contourner le système. Par exemple, il est possible d’introduire subrepticement des axiomes supplémentaires lors de la formalisation, de mal formaliser l’énoncé du problème, ou de profiter de comportements « marginaux » de la bibliothèque mathématique ou de la syntaxe. Il faut être particulièrement vigilant si la preuve formelle est anormalement courte ou anormalement verbeuse.

En résumé, selon Terence Tao, les avancées de l’IA sur les problèmes d’Erdős méritent l’attention, mais ce qui compte vraiment, ce sont le niveau de difficulté du problème, la vérification bibliographique, la restitution de l’énoncé, l’intégration des connaissances et la solidité de la chaîne de validation, entre autres indicateurs multidimensionnels.

Le fait que l’IA arrive à des résultats ne signifie pas qu’elle possède déjà des capacités mathématiques complètes.

Concrètement, que fait réellement l’IA ?

La page GitHub de Terence Tao classe les contributions de l’IA en plusieurs catégories.

Certaines IA ont généré des solutions complètes (ou partielles), d’autres pensaient que le problème était non résolu alors que la littérature l’avait déjà traité, certaines ont participé à la recherche bibliographique, d’autres ont formalisé des preuves dans Lean, d’autres encore ont aidé à réécrire des arguments existants, etc.

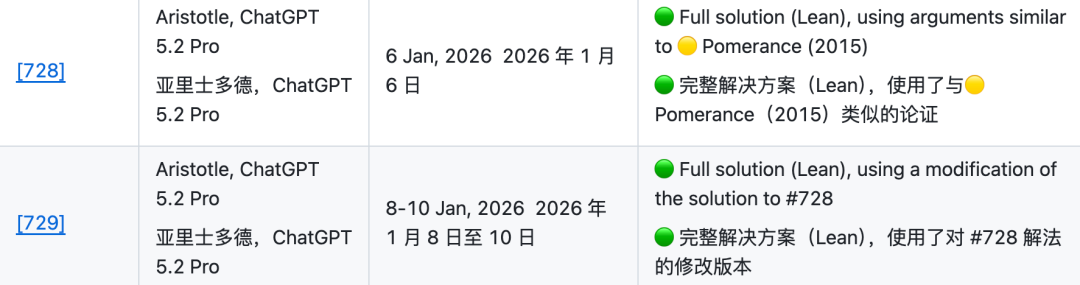
Par exemple, la page indique que le problème #728 a été entièrement résolu (vérification Lean) le 6 janvier 2026 par Aristotle et ChatGPT 5.2 Pro,problème #729 ayant également reçu une solution complète (vérification Lean) du 8 au 10 janvier.

Cela signifie que pour certains types et niveaux de difficulté de problèmes, l’IA peut effectivement produire une « structure de preuve opérationnelle », voire intégrer le processus de vérification formelle.

Certains problèmes ont été entièrement résolus par l’IA, mais on s’est ensuite rendu compte que quelqu’un l’avait déjà fait auparavant.

Terence Tao a également créé une catégorie « revue de littérature assistée par IA » : l’IA est utilisée pour vérifier l’existence de solutions ou d’erreurs d’étiquetage « Open ».

Se fier à quelques exemples isolés pour conclure que « l’IA est invincible en mathématiques » est manifestement réducteur.

Mais à l’inverse, penser que l’IA est totalement incapable en mathématiques, c’est aussi passer à côté de ce qu’elle a réellement à offrir.

Une affirmation plus juste serait : l’IA apprend à prendre en charge les tâches répétitives et techniques des mathématiques : appliquer des schémas, combler les lacunes, formaliser, rédiger/réviser des textes, consulter la littérature.

Mais la véritable « âme » des mathématiques — poser des questions profondes, créer de nouveaux concepts, intégrer un résultat dans le réseau de connaissances d’une discipline — dépend toujours fortement de l’humain.

Et c’est précisément ce que Terence Tao a voulu exprimer dans son post nocturne.

Le mathématicien du futur ne sera peut-être plus un penseur solitaire, mais le chef d’une armée d’intelligences silicium : sur l’immense plaine des mathématiques, l’humain trace la voie, l’IA construit ponts et routes.

Ne mythifiez pas l’IA hors de son contexte, mais ne sous-estimez jamais non plus cette force qui est en train de transformer la manière dont nous explorons la vérité.